The Physics of How Microbubbles Sort Cells
Flotation is the driving principle behind our cell sorting technology. It’s hard to imagine many other physical phenomena that humans have more of an intuition for than floating and sinking. The exact same rules of floating and sinking apply to a stem cell being lifted from a sample on the back of Akadeum’s microbubbles. In principal, it is as simple as pair of water wings that keeps a two-year-old child afloat in a swimming pool.
Understanding these rules lets you anticipate important performance features of separation systems like ours. It allows for questions like these to be answered:
- How long will it take for my cells to get to the top of the tube? (Not long.)
- Can microbubbles lift a spheroid? (Probably.)
- How many microbubbles do you need to float a large cell? (One.)
The answer to these questions may have a big impact on the success of your cell separations, and so flotation is where we will start.
Why Do Microbubbles Float?

Archimedes of Syracuse
Archimedes of Syracuse gets credit for figuring out the means of determining whether an object in a liquid will sink or float.
In short, if the density of an object is less than the density of the liquid it displaces, the object will float. Otherwise, the object will be either neutrally buoyant or will sink.
For us, whether an object floats or sinks is not enough. Rather, we want to know things like how quickly a microbubble will move through a user’s sample, especially if that bubble is carrying a cellular payload.

Sir George Stokes
For that question, we turn to Sir George Gabriel Stokes. Stokes is one of the fathers of modern fluid dynamics, which may in part explain his stern expression.
Relevant to microbubbles, his law identifies these features:
- The difference in density between the bubble and the surrounding fluid: The greater the density difference, the faster the upward velocity.
- The radius of the bubble: At a given density, the larger the bubble, the faster it rises.
- The gravitational or centrifugal force applied: For bubbles separating cells on the benchtop, only gravity acts on the bubbles. By placing the sample in a centrifuge, g can be increased many times, for good or for ill depending on your application.
These three elements can all be controlled experimentally through your choice of microbubble and your use of a centrifuge. For completeness’ sake, a fourth feature, the sample viscosity, is also important but is not readily modified by most users (including us).
How Quickly Do Microbubbles Lift Cells?
Stokes’ Law addresses a special (but highly relevant) circumstance in which fluid is moving around a sphere in a nonturbulent way. As a user of cells, you might be able to violate the nonturbulent assumption, but you’d probably significantly damage your cells in the process.
Under this assumption, the buoyant force experienced by the microbubble, which we’ll call FB, can be expressed as follows:
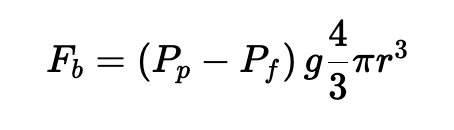
where ρp is the density of the microbubbles in kg/m3, ρf is the density of water, g is the acceleration due to gravity or centrifugation in m/s2, and r is the radius of the microbubble in meters.
To predict the rate of rise, the buoyancy is not enough—you also need to include the drag experienced by the bead as well:
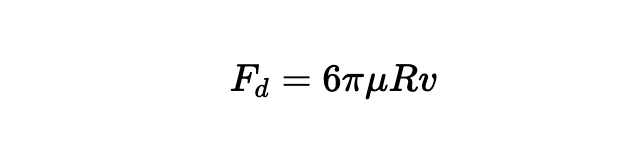
where μ is the dynamic viscosity of water, typically ~ 10-4 Pa-s, and V is the velocity of the beads in m/s.
The terminal velocity, which is the highest speed with which a particle of a given density can rise in a fluid of given viscosity, can be reached algebraically by setting FB = FD (the condition under which any additional buoyancy of the bead is completely counteracted by additional drag) by solving for V :
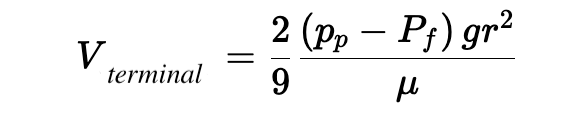
This equation sums up a lot of what you’ll need to have a working intuition about our microbubbles, specifically that the velocity at which bubbles will rise in your sample is:
- Linearly related to the difference in density between the bubble and the surrounding fluid
- Linearly related to the gravitational (or centrifugal) force applied to the sample
- Proportional to the square of the bubble radius, meaning that small changes in bubble dimension can have outsize effects on rise time
The other physical feature in these equations—the viscosity of the sample—is not for most users a controllable feature, but for completeness’ sake, it does impact microbubble velocity.
For our microbubbles, in the absence of an attached cell, the typical maximum rising velocity is just shy of 1 mm/min. In practice, the observed velocity is substantially more. Learn more about Buoyancy Activated Cell Sorting (BACS).